Nem értem, mert programozóként a "szimulációs" program megírása után elég szimplának vélhető a valószínűségi modell (de persze amikor így érzek, nem felejthetem el, hogy rám is jellemző a wigneri észrevétel az általános emberi tulajdonságról).

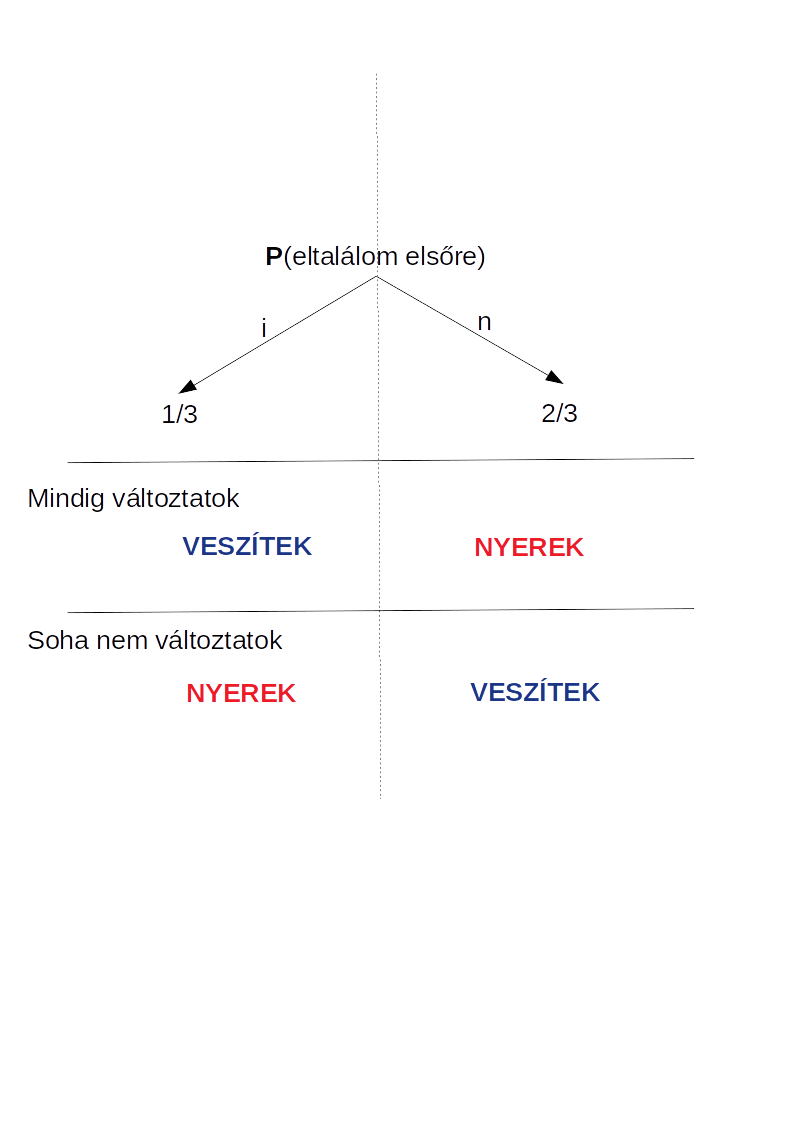
Magával a Monty Hall problémával idén nyáron találkoztam a gyerekekkel egy ebéd közben, amikor is a 21 Las Vegas ostroma filmet néztük, melyben az MIT matek profja az ígéretes "számolónak" szegezi a kérdést, hogy van három ajtó, az egyik mögött egy értékes ajándék, a másik kettő mögött semmi. Melyiket választja? 1/3 valséggel az egyiket, okés. Aztán a riporter a három ajtó közül kinyit egy olyat, mely mögött semmi nincs és a játékosnak szegezi a kérdést, hogy fenntartja az eredeti választását, avagy megváltoztatja?

Ezen rész után megállítottam a filmet (amit éppen azért tettem be, hogy a gyerekek matek iránti vonzalmát növeljem).

A gyerekek - szerintem - elfogadva a filmben a "narrátor" sugallatát, a főhős változtat döntését intuítíven elfogadták és nem értették én mit agyalok rajta... miért nem nézzük már tovább... a film után aztán magam is beláttam, ha nem is mély meggyőződésből, de annyival lezárva, hogy ha nem találja el elsőre, akkor előnyösebb helyzetbe kerül a kinyitott második ablak infóval, mert ekkor a műsorvezetőnek nincs választása, csak egyet nyithat, a játékos meg ezt "tudva" ugyanúgy "ismeri" a nyeremény helyét és mivel rosszul dönteni elsőre 2/3-ad, így változtatni a "nyerő strat" valóban.

Aztán a tegnap felütöttem a Paul Hoffman Erdősről szóló könyvét, amelyben részletesen lesztorizza, hogy Erdős Pál hogyan reagált a problémára: engem megnyugtatott, hogy elsőre az ő intuíciója is mást súgott! A könyvbeli leírás alapján viszont meglepő, hogy a szimulációs program kimenetének tanulmányozása után is elégedetlen volt és sürgette a Nagykönyvi belátás szükségességét...

Ez adta az inspirációt, hogy a Bátf41 Haxor Stream tűzze műsorra a program megírását (mert ugye Chaitin után valljuk, hogy "csak azt értjük igazán, amit be tudunk programozni").

Az R szimulációs kód

#   An illustration written in R for the Monty Hall Problem 
#   Copyright (C) 2019  Dr. Norbert Bátfai, nbatfai@gmail.com
#
#   This program is free software: you can redistribute it and/or modify
#   it under the terms of the GNU General Public License as published by
#   the Free Software Foundation, either version 3 of the License, or
#   (at your option) any later version.
#
#   This program is distributed in the hope that it will be useful,
#   but WITHOUT ANY WARRANTY; without even the implied warranty of
#   MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#   GNU General Public License for more details.
#
#   You should have received a copy of the GNU General Public License
#   along with this program.  If not, see <http://www.gnu.org/licenses/>

kiserletek_szama=10000000
kiserlet = sample(1:3, kiserletek_szama, replace=T)
jatekos = sample(1:3, kiserletek_szama, replace=T)
musorvezeto=vector(length = kiserletek_szama)

for (i in 1:kiserletek_szama) {

    if(kiserlet[i]==jatekos[i]){
    
        mibol=setdiff(c(1,2,3), kiserlet[i])
    
    }else{
    
        mibol=setdiff(c(1,2,3), c(kiserlet[i], jatekos[i]))
    
    }

    musorvezeto[i] = mibol[sample(1:length(mibol),1)]

}

nemvaltoztatesnyer= which(kiserlet==jatekos)
valtoztat=vector(length = kiserletek_szama)

for (i in 1:kiserletek_szama) {

    holvalt = setdiff(c(1,2,3), c(musorvezeto[i], jatekos[i]))
    valtoztat[i] = holvalt[sample(1:length(holvalt),1)]
    
}

valtoztatesnyer = which(kiserlet==valtoztat)


sprintf("Kiserletek szama: %i", kiserletek_szama)
length(nemvaltoztatesnyer)
length(valtoztatesnyer)
length(nemvaltoztatesnyer)/length(valtoztatesnyer)
length(nemvaltoztatesnyer)+length(valtoztatesnyer)

Az R kód futtatása

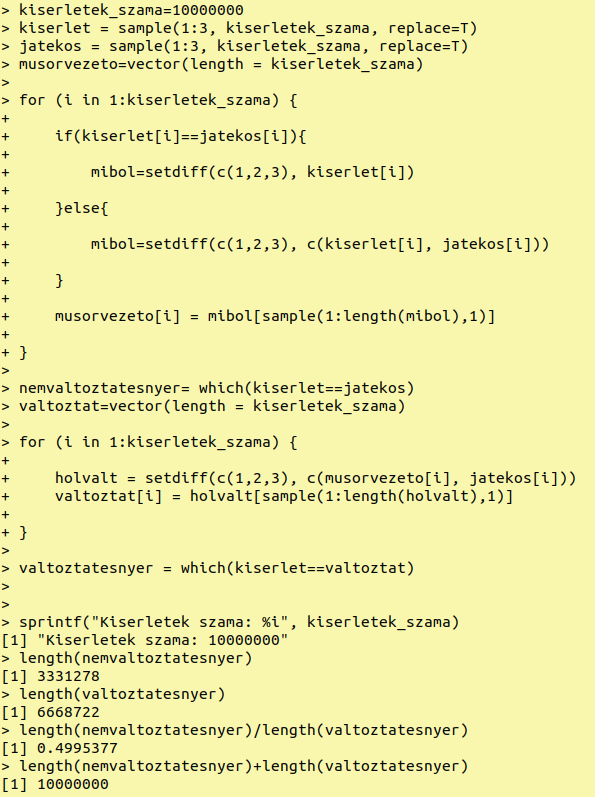
Az R átgondolása